Quantum Computing in AI
1. what is Quantum Computing in AI?

Quantum Computing in AI refers to the use of quantum computing technologies to enhance and accelerate artificial intelligence (AI) processes. Quantum computing is based on the principles of quantum mechanics, such as superposition, entanglement, and quantum parallelism, which allow quantum computers to process and analyze vast amounts of data much faster than classical computers. In the context of AI, quantum computing has the potential to solve complex problems that are difficult or even impossible for classical computers to handle efficiently. The integration of quantum computing into AI could lead to breakthroughs in areas like machine learning, optimization, data analysis, and pattern recognition, pushing the boundaries of what is currently achievable in AI.
One of the most significant ways quantum computing can benefit AI is through its ability to process large datasets with quantum algorithms that can exploit quantum parallelism. Quantum machine learning (QML) is an emerging field that combines the principles of quantum computing and machine learning. Quantum algorithms can potentially speed up tasks such as data classification, clustering, and pattern recognition, enabling AI models to be trained on larger datasets more efficiently. For example, quantum versions of traditional machine learning algorithms, such as support vector machines (SVMs) or k-means clustering, could offer exponential speedups over their classical counterparts by leveraging quantum entanglement and superposition, allowing for faster and more accurate model training.
Additionally, quantum computing could improve optimization problems in AI. Many AI tasks, such as training neural networks or finding the optimal configuration of a machine learning model, involve complex optimization problems that require significant computational resources. Quantum computers can solve certain types of optimization problems exponentially faster than classical computers by using quantum algorithms like quantum annealing or Grover's algorithm, which offer more efficient search techniques for optimal solutions. This could lead to AI systems that are better at making predictions, decision-making, and solving complex real-world problems, such as in drug discovery, financial modeling, or supply chain optimization.
2.Quantum Machine Learning
Quantum Machine Learning
is an interdisciplinary field that combines the principles of quantum computing and machine learning (ML) to develop algorithms that can solve problems more efficiently than classical machine learning algorithms. In traditional machine learning, data is processed by classical computers using algorithms such as supervised learning, unsupervised learning, or reinforcement learning. However, the complexity and scale of some machine learning problems, particularly with large datasets, can become computationally expensive and time-consuming. Quantum computing, with its ability to process vast amounts of data simultaneously due to quantum superposition and entanglement, has the potential to accelerate and enhance machine learning tasks, providing exponential speed-ups and solving problems that are intractable for classical computers.
One of the key features of quantum machine learning is the ability to leverage quantum parallelism, where quantum computers can process multiple inputs simultaneously. This can significantly speed up certain machine learning algorithms, particularly those that involve searching large datasets or performing complex optimization tasks. For example, quantum algorithms like Quantum Support Vector Machines (QSVM), Quantum K-Means Clustering, and Quantum Principal Component Analysis (QPCA) are designed to speed up traditional machine learning tasks. These algorithms exploit quantum entanglement and superposition to perform data analysis more efficiently than classical counterparts. In practice, these quantum-enhanced machine learning techniques could be applied in fields like drug discovery, financial modeling, natural language processing, and computer vision.
Another important advantage of quantum machine learning is its ability to handle large, high-dimensional datasets with quantum data encoding. Classical computers struggle to process such data, especially when it is too large or complex for existing algorithms. Quantum computers, however, can represent and manipulate high-dimensional data in ways that classical computers cannot. Quantum machine learning algorithms can perform operations like quantum feature mapping, where quantum states encode classical data into quantum bits (qubits) in a high-dimensional space. This allows quantum machine learning models to uncover patterns or structures within the data that would otherwise be difficult for classical models to detect. Quantum-enhanced optimization algorithms, like Quantum Annealing, can also help in optimizing machine learning models and making them more efficient by quickly finding the best model parameters.

3. Quantum Neural Networks
Quantum Neural Networks
are an emerging field at the intersection of quantum computing and neural networks, combining the principles of quantum mechanics with the structure of classical neural networks to potentially enhance machine learning capabilities. A neural network is a computational model inspired by the human brain, consisting of layers of interconnected nodes (neurons) that process data to recognize patterns, make predictions, and classify information. While classical neural networks, including deep learning models, have been highly successful in various applications, they require significant computational resources, particularly when dealing with large datasets or complex problems. Quantum computing offers the possibility of overcoming these challenges by harnessing quantum properties such as superposition, entanglement, and quantum parallelism to process information more efficiently..
Quantum Neural Networks aim to replicate the functionalities of classical neural networks but with the added advantage of quantum computational power. One of the primary goals of QNNs is to take advantage of quantum entanglement and superposition to process and analyze information in a highly parallel and efficient manner. For example, in a classical neural network, the data processing through layers of neurons is sequential, meaning each layer has to wait for the previous layer's output before proceeding. In contrast, QNNs can perform computations in parallel due to quantum superposition, where quantum bits (qubits) can exist in multiple states simultaneously. This parallelism allows quantum neural networks to explore a broader range of solutions at once, potentially speeding up the learning process and improving the ability to solve complex problems.
One of the key challenges in quantum neural networks is the quantum-classical hybrid model, where classical neural networks and quantum computers are used together to leverage the strengths of both. Many proposed quantum neural network models rely on quantum circuits to perform the complex computations needed for certain operations, such as weight updates in training, while still maintaining some classical components, like data input and final predictions. These hybrid quantum-classical models can potentially overcome current hardware limitations in quantum computing, where quantum computers are still relatively noisy, error-prone, and have a limited number of qubits. Some quantum algorithms, such as the Quantum Approximate Optimization Algorithm (QAOA) and Variational Quantum Eigensolver (VQE), have been explored to train quantum neural networks by minimizing a cost function related to the model’s predictions, similar to how backpropagation works in classical neural networks
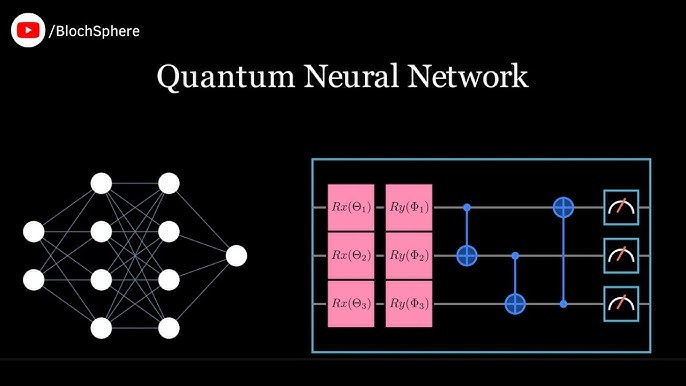
4.Hybrid Classical-Quantum AI
Hybrid Classical-Quantum AI
refers to the integration of classical computing methods with quantum computing technologies to enhance the performance of artificial intelligence (AI) systems. In this approach, classical computers handle certain tasks or computations that are more efficient on classical hardware, while quantum computers are used for tasks that can benefit from quantum parallelism, superposition, and entanglement. The hybrid model seeks to combine the strengths of both classical and quantum systems, leveraging quantum computing's potential to solve specific problems that are difficult or infeasible for classical machines to handle, while still utilizing the efficiency, reliability, and well-established infrastructure of classical computing for other tasks.
One of the main challenges in AI is dealing with the exponential growth of complexity as the size of datasets and the number of variables increases. Classical AI techniques, such as deep learning and machine learning, require large amounts of computational power to process high-dimensional data, perform optimization, and train models effectively. Quantum computing, on the other hand, has the potential to revolutionize AI by offering speedups in specific areas, particularly in optimization and large-scale data analysis. For example, quantum algorithms such as Quantum Approximate Optimization Algorithm (QAOA) and Grover’s algorithm can potentially accelerate tasks such as finding optimal solutions in combinatorial problems or searching large datasets, tasks that are notoriously challenging for classical machines.
A hybrid classical-quantum AI system typically involves using quantum computers for specific parts of an AI model or task that are computationally expensive or require handling high-dimensional datasets. One common application is in quantum machine learning (QML), where quantum computers are used to speed up machine learning algorithms like support vector machines (SVMs), clustering, and dimensionality reduction. The classical component of the AI system handles the data preprocessing, input/output management, and interpretation of results, while the quantum component handles the heavy computational lifting. This hybrid approach allows the system to benefit from the strengths of quantum algorithms without the need for fully quantum-based AI systems, which are still in the early stages of development and face challenges such as noise and error rates in quantum hardware.

5.Optimization Problems in AI
Optimization Problems in AI
are critical challenges in artificial intelligence where the goal is to find the best possible solution or outcome from a set of possible options. Optimization is an essential part of machine learning, neural networks, and other AI-based techniques, as it is used to improve the performance of models by fine-tuning parameters, minimizing errors, and maximizing accuracy. Optimization problems are often encountered in tasks like training machine learning models, designing efficient algorithms, and solving real-world decision-making challenges. These problems typically involve finding an optimal solution under a set of constraints, and solving them efficiently is key to making AI systems faster, more reliable, and more accurate.
In machine learning, optimization primarily refers to the process of adjusting model parameters (like weights in neural networks) to minimize a given loss or cost function. This is known as training a model. For instance, in supervised learning, the model learns to predict outcomes based on input data, and during training, optimization techniques are used to adjust the model’s parameters to minimize the difference between predicted and actual outcomes (the loss function). Common optimization algorithms used in machine learning include gradient descent, stochastic gradient descent (SGD), and more advanced methods like Adam. These methods adjust the parameters iteratively to find the minimum of the cost function. The challenge in optimization lies in dealing with local minima, overfitting, and ensuring that the algorithm converges to the global optimum, especially in complex models like deep neural networks.
Combinatorial optimization is another type of optimization problem in AI, where the goal is to select the best combination of variables under a set of constraints. Problems like the Traveling Salesman Problem (TSP) or Knapsack Problem fall into this category. These types of problems are generally NP-hard, meaning they cannot be solved in polynomial time for large datasets. For such problems, AI techniques like genetic algorithms, simulated annealing, and ant colony optimization are often used. These algorithms aim to find good solutions within a reasonable time, rather than guaranteeing the exact optimal solution, due to the high computational cost of solving large-scale combinatorial problems. These optimization methods often involve heuristics or approximation algorithms that work well for practical purposes, even if they do not guarantee perfect solutions.

6.AI Model Training with Quantum Computing
AI Model Training with Quantum Computing
refers to the use of quantum computing techniques to enhance the training of artificial intelligence models, particularly in machine learning tasks. The training process in AI involves adjusting model parameters to minimize a given loss function, typically through optimization techniques like gradient descent. However, as AI models, especially deep learning networks, become more complex, training them becomes computationally expensive and time-consuming. This is where quantum computing comes into play, offering the potential to speed up training processes, handle larger datasets, and solve optimization problems more efficiently.
One of the main advantages of quantum computing in AI training lies in its ability to process information in parallel, leveraging quantum phenomena like superposition and entanglement. Quantum superposition allows quantum bits (qubits) to represent multiple states simultaneously, enabling quantum computers to evaluate multiple solutions at once. This parallelism can significantly speed up tasks like optimization, a key component of training AI models. For example, quantum algorithms like Quantum Gradient Descent (QGD) or Quantum Approximate Optimization Algorithm (QAOA) could be used to optimize the weights of a neural network much faster than classical counterparts. Quantum-enhanced optimization methods can explore the solution space more effectively, potentially avoiding local minima and finding better global solutions, which is a challenge in classical machine learning methods.
Another potential benefit of using quantum computing for AI model training is its ability to handle large-scale, high-dimensional data. Classical machines struggle with the exponential growth of complexity when dealing with datasets that have many features or variables. Quantum computing, however, has the potential to manage high-dimensional data much more efficiently due to its ability to represent and process large datasets through quantum states. For instance, quantum computers could use quantum feature maps to encode classical data into quantum states, allowing them to perform tasks like dimensionality reduction or data compression more effectively. This capability could allow AI models to learn patterns in large, complex datasets that classical computers would struggle to process.

7.Reinforcement Learning in Quantum Systems
Reinforcement Learning in Quantum Systems
is an emerging field that combines the principles of reinforcement learning (RL) and quantum computing to enhance the learning and decision-making capabilities of AI agents. Reinforcement learning, in classical AI, involves an agent interacting with an environment, taking actions, and receiving rewards or penalties based on the actions. The goal is for the agent to learn an optimal policy that maximizes its cumulative reward over time. Quantum systems, leveraging quantum mechanics, bring powerful tools like quantum superposition, entanglement, and quantum parallelism, which can be applied to speed up learning processes, handle complex decision spaces, and improve optimization tasks in RL
In traditional classical reinforcement learning (RL), algorithms like Q-learning and policy gradients rely on iteratively adjusting the agent’s policy or value function. These classical algorithms often struggle with large state and action spaces, particularly when solving complex or high-dimensional problems. Quantum reinforcement learning (QRL) aims to overcome these limitations by utilizing quantum computers to represent and manipulate vast quantities of data simultaneously. The inherent parallelism of quantum systems allows quantum RL algorithms to process multiple possibilities at once, potentially finding optimal strategies in less time than classical RL methods.
Quantum RL algorithms typically involve using quantum computing for various tasks within the RL process, such as optimizing policies, enhancing exploration strategies, and speeding up learning. For example, Quantum Q-learning is a quantum version of the classical Q-learning algorithm where quantum computers are used to update the Q-values (the expected future rewards of a given state-action pair) more efficiently. Quantum states can represent multiple action-value pairs simultaneously, allowing for faster exploration and better decision-making, which is particularly useful in environments with large or continuous state spaces. Quantum systems could also be employed to improve exploration-exploitation trade-offs, allowing RL agents to balance the exploration of new actions and the exploitation of known, rewarding actions more efficiently.
8.Quantum Pattern Recognition
Quantum Pattern Recognition refers to the application of quantum computing techniques to the problem of identifying patterns or regularities in data, which is a key aspect of many machine learning tasks, including classification, anomaly detection, and clustering. In classical machine learning, pattern recognition is used to learn relationships and structures in data by training models on large datasets. The idea behind quantum pattern recognition is to exploit the unique capabilities of quantum computers, such as quantum superposition, entanglement, and quantum parallelism, to potentially accelerate and improve the process of recognizing complex patterns that are difficult for classical systems to handle.
One of the primary advantages of quantum pattern recognition is its ability to represent and process information in high-dimensional spaces efficiently. Classical computers encode data in binary format, and as the dimensionality of the data increases, the computation needed to process that data grows exponentially. Quantum computers, however, can encode data in quantum states that exist in a superposition of multiple configurations, which enables them to represent and process high-dimensional data more compactly. For example, quantum feature mapping techniques can be used to map classical data into a higher-dimensional quantum space, where patterns in the data may become easier to detect and learn. This enhanced capability allows quantum systems to tackle pattern recognition problems that would be computationally prohibitive for classical computers
Quantum algorithms like Quantum Support Vector Machines (QSVMs) and Quantum k-means clustering are examples of quantum techniques being explored for pattern recognition tasks. In the case of QSVM, quantum computers are used to perform the classification task by finding hyperplanes in a quantum space that best separate different classes of data. Quantum computers can process more complex kernels than classical SVMs, allowing for better separation of classes in high-dimensional feature spaces. Similarly, Quantum k-means clustering uses quantum computers to perform clustering of data into groups based on their similarity, but with quantum speedups that could make the process faster and more efficient for large datasets. These quantum-enhanced methods could potentially outperform their classical counterparts in terms of speed and accuracy when dealing with complex or large-scale datasets.
Quantum Pattern Recognition refers to the application of quantum computing techniques to the problem of identifying patterns or regularities in data, which is a key aspect of many machine learning tasks, including classification, anomaly detection, and clustering. In classical machine learning, pattern recognition is used to learn relationships and structures in data by training models on large datasets. The idea behind quantum pattern recognition is to exploit the unique capabilities of quantum computers, such as quantum superposition, entanglement, and quantum parallelism, to potentially accelerate and improve the process of recognizing complex patterns that are difficult for classical systems to handle.
One of the primary advantages of quantum pattern recognition is its ability to represent and process information in high-dimensional spaces efficiently. Classical computers encode data in binary format, and as the dimensionality of the data increases, the computation needed to process that data grows exponentially. Quantum computers, however, can encode data in quantum states that exist in a superposition of multiple configurations, which enables them to represent and process high-dimensional data more compactly. For example, quantum feature mapping techniques can be used to map classical data into a higher-dimensional quantum space, where patterns in the data may become easier to detect and learn. This enhanced capability allows quantum systems to tackle pattern recognition problems that would be computationally prohibitive for classical computers
Quantum algorithms like Quantum Support Vector Machines (QSVMs) and Quantum k-means clustering are examples of quantum techniques being explored for pattern recognition tasks. In the case of QSVM, quantum computers are used to perform the classification task by finding hyperplanes in a quantum space that best separate different classes of data. Quantum computers can process more complex kernels than classical SVMs, allowing for better separation of classes in high-dimensional feature spaces. Similarly, Quantum k-means clustering uses quantum computers to perform clustering of data into groups based on their similarity, but with quantum speedups that could make the process faster and more efficient for large datasets. These quantum-enhanced methods could potentially outperform their classical counterparts in terms of speed and accuracy when dealing with complex or large-scale datasets.

Comments